Product added to cart
- Início
- Blog
- Libus Comunica
- Nível De Proteção Em Proteção Auditiva

Os índices de atenuação dependem de um parâmetro de natureza estatística denominado nível de proteção. Este parâmetro deve ser interpretado como a percentagem de utilizadores a quem é assegurada a proteção mínima especificada pelo índice que caracteriza o protetor auditivo em questão.
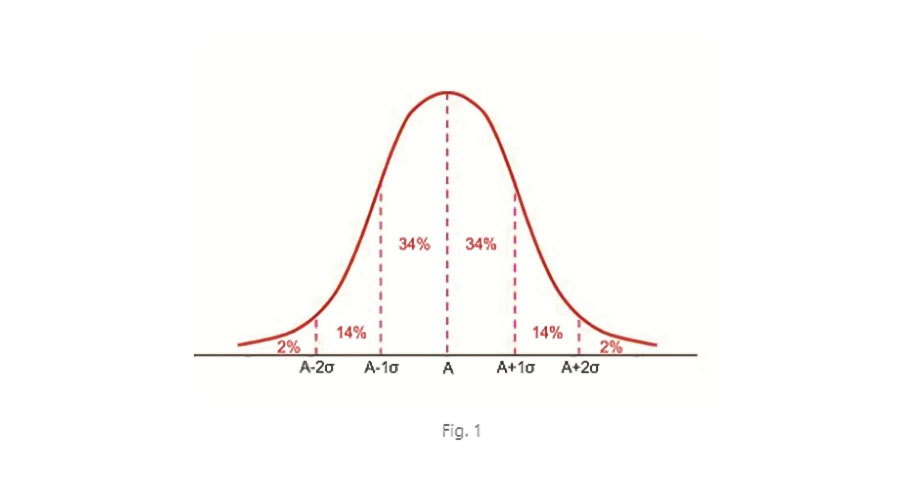
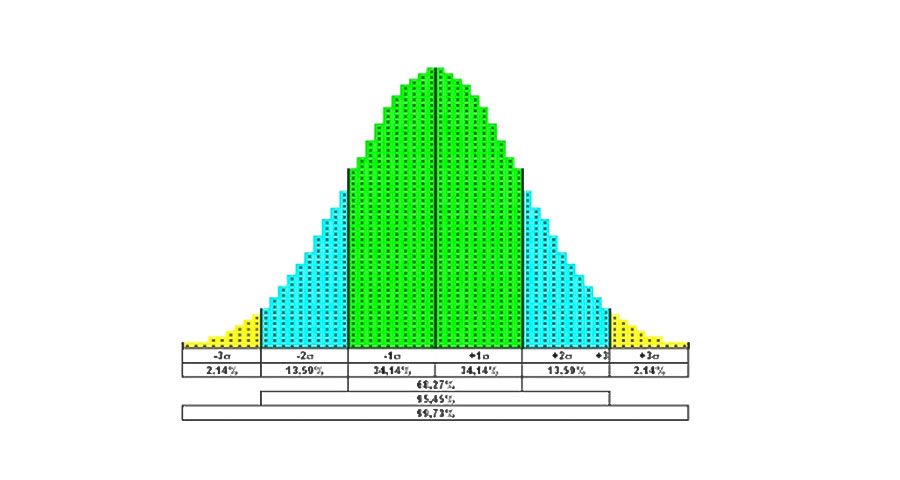
A maioria dos processos naturais respondem a uma distribuição de probabilidade denominada normal ou gaussiana (veja a imagem abaixo). A atenuação de um protetor auditivo em uso também. Se consideramos um protetor com uma atenuação média A e um desvio padrão σ, o gráfico de sua função de densidade de probabilidade é como o da figura da direita. As propriedades de uma distribuição normal, sabemos que é entre ± 1σ se encontra em 68% da população e entre ± 2σ em 96% (34+14+34+14) como se vê na fig. 1. O restante da população (4%) se encontra desde ± 2σ até o infinito. Obviamente, a soma de todos é de 100%, em total da população.
Se fabricarmos um lote de protetor auditivo com atenuação média A, podemos dizer que apenas 50% dos usuários estarão protegidos por essa atenuação, mas a população se encontra acima desse valor médio (A+1σ, A+2σ, etc.) como mostra a fig. 2.

Se queremos garantir um nível de proteção em maior quantidade de usuários devemos assumir uma margem de segurança maior de atenuação.
Se subtrairmos 1σ da atenuação média, podemos dizer que o protetor fornecerá uma atenuação de pelo menos A-1σ.
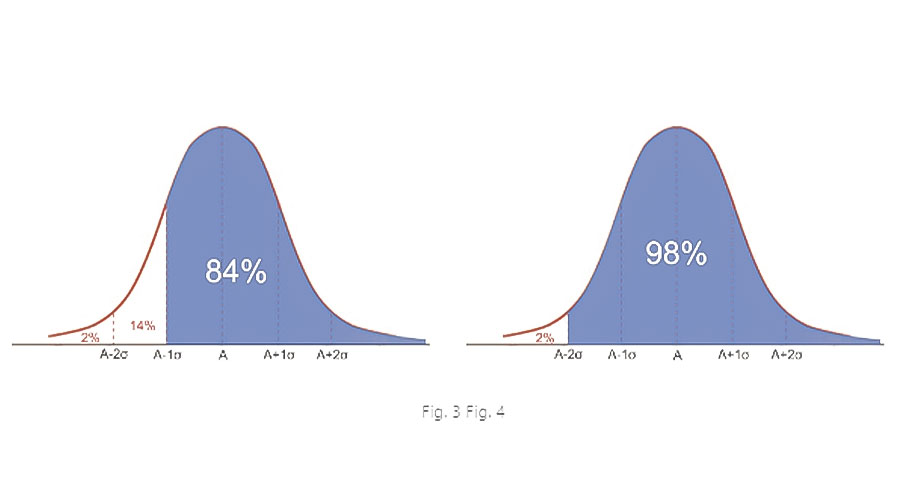
Restando 2σ asseguramos uma atenuação mínima de A-2σ al 98% de todos os usuários que utilizem corretamente o protetor (fig. 4).
Como vimos na ficha técnica, ou cálculo do NRR, 2 desvios-padrão são subtraídos, ou seja, leva em conta 98% dos usuários.
O NRRsf subtrai 1 desvio padrão, por isso inclui 84% dos usuários.
A SNR é uma formulação para ser calculada para diferentes níveis de proteção (se bem 84% é o habitual). O maior nível desejado maior será o número de desvio padrão que teremos que restar ao valor médio de atenuação en cada octava; llamando α al multiplicador y siendo α * σ el valor a restar::
Anexo - Conceptos de Probabilidade, Estatística e Distribuição Normal - Eng. Adrián Balonga / Chefe de Laboratório de LIBUS S.A.
Probabilidade y Estadística
As análises dos eventos governados pela probabilidade se chamam estatística. A estatística é uma ferramenta indispensável para a tomada de decisões, visualizar a probabilidade de um evento é simplesmente tentar determinar a prioridade de frequência que vai ser produzida. Dada a sua natureza aleatória, o futuro é sempre incerto. Quando não existe certeza do resultado de um evento, podemos falar sobre probabilidade de certos resultados, dependendo da frequência que ocorrem sobre esse conhecimento histórico para fazer preposições. Na década de 1560, Gerolamo Cardano escreveu o primeiro tratado sobre probabilidade.
Pierre Laplace lançou as bases da teoria analítica da probabilidade. Ele foi o primeiro a afirmar que, dado qualquer resultado x, dentro de um conjunto finito de N resultados possíveis, onde nenhum tem mais chance de ocorrer do que outro, a probabilidade de x ocorrer é:
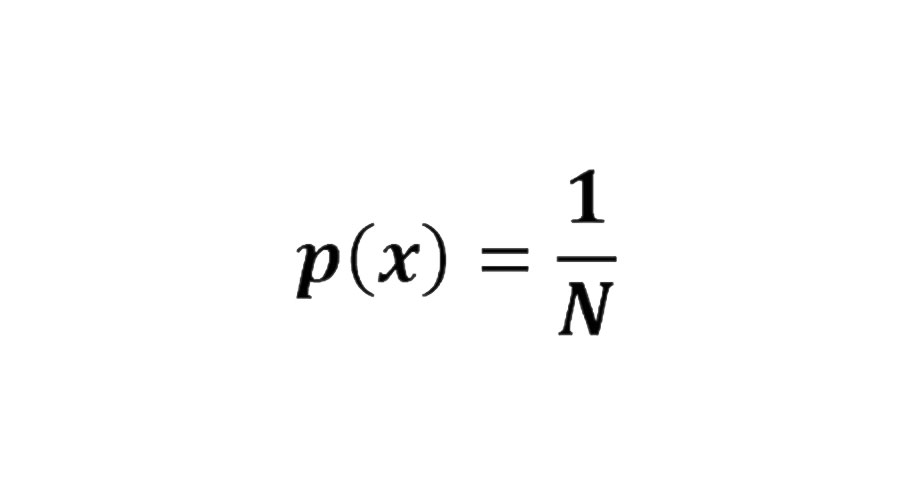
Estadística: É um ramo da matemática, relacionado ao estudo de fenômenos aleatórios cujo resultado é imprevisível e é a forma de tomar decisões razoáveis baseadas em observações prévias de alguns fenômenos;
População: Na estatística, é um conjunto de resultados, elementos, indivíduos, objetos ou fenômenos que apresentam características comuns que se desejam estudar;
Histograma: Na estatística, é uma representação gráfica de uma variável em forma de barras, onde a altura de cada barra é proporcional a frequência de repetição dos valores em certos intervalos.
Suponhamos que sou fabricante de pratos e eles devem ter um determinado peso objetivo. Para determinar qual tolerância de peso pode ser comportado ao fabricá-los, meço este parâmetro com uma balança para cada um dos pratos do lote. Feito isso, deixo-os em pilhas para que consiga medir o peso e saber a média. Como na imagem abaixo:

Isso que vemos é um histograma de peso dos pratos fabricados, é a “primeira vista” da distribuição da população.
Distribuição Normal o Gaussiana
A distribuição normal foi apresentada por Abraham de Moivre em um artigo de 1733. O nome de Gauss é associado a esta distribuição porque o uso com precisão quando analisa dados astronômicos. A distribuição normal, é normalmente chamada “Campanha de Gauss” e tem uma grande importância em muitos ramos da ciência, porque permite caracterizar fenômenos naturais, sociais e psicológicos.
A maioria dos fenômenos que se qualificam com uma variável contínua com as dimensões (peso, altura, intensidade, etc) seguem uma distribuição normal. A distribuição normal é mais estendida porque muitos ensaios estatísticos são baseados em uma “normalidade”, mais ou menos justificada de uma variável aleatória de estudo.
Para entender melhor a distribuição Gaussiana, é interessante observar uma “máquina de Galton”, nela deixam cair uma grande quantidade de bolinhas (que representam a população) que vão encontrando obstáculos conforme vão caindo (que representam as fontes de variação ou dispersão) que as obrigaram a se desviar de sua trajetória com a probabilidade de 50% para a esquerda ou direita. Vídeo explicativo: (https://www.youtube.com/watch?v=8AD7b7_HNak)
São 2 parâmetros caracterizam a distribuição normal:
A meia[m]: se calcula como a média aritmética dos dados e corresponde ao centro da campanha.
O desvio padrão [σ]: se calcula como a raiz quadrada da média da diferença de cada valor com o médio elevado ao quadrado e é uma medida relativa do ancho de campanha.
O dado mais útil que nos informa é como se distribui a população (área abaixo da curva):
- Em 68,27% se encontra dentro do intervalo de ±1σ
- el Em 95,45% se encontra dentro do intervalo de ±2σ
- Em 99,73% se encontra dentro do intervalo de ±3σ

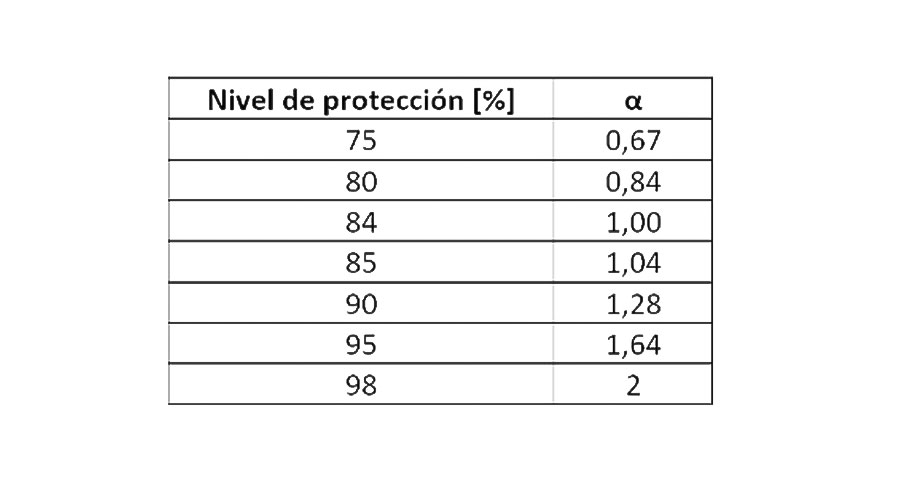
Toda vez que nos encontramos frente a incerteza em relação a uma medida ou fenômeno natural de características contínuas (pode ser medido em uma escala graduada) e não temos informações sobre sua distribuição, assumindo que ele é distribuído de acordo com o normal é a melhor opção. E se devemos dar um índice de confiança em relação a um valor medido, é comum tomar um determinado fator de cobertura em termos de desvios-padrão, como mostrado na tabela.
Categorias
- Libus Service (0)
- Proteção Ao Soldador (0)
- Workshop (0)
- Eventos (0)
- Libus Comunica (7)
- Proteção Craniana (1)
- Proteção respiratória (2)
Posts Recentes



 LAT
LAT








